Variation in position of the focal plane of an eyepiece relative to the external shoulder.
Orwell Astronomical Society (Ipswich)
The Barlow Lens
Peter Barlow (1776 - 1862), an instructor at the Royal Military Academy in Woolwich, south-east London, discovered that placing a negative focal length (concave or diverging) lens inside the focal plane of the objective of a telescope, just in front of the eyepiece, increased the effective focal length of the instrument. Because the magnification of a telescope is directly proportional to its focal length, the effect is to increase the magnification. The formula for the increase is:
M = 1 + (x / f),
where M is the Barlow amplification factor, x is the distance between the Barlow lens and the new focal plane, and f is the focal length of the Barlow lens. (Of course, x and f must be expressed in the same units.)
Thus, for a 2x Barlow, the distance between the centre of the Barlow lens and the focal plane of the eyepiece is equal to the focal length of the Barlow lens. One way of determining the focal length of a Barlow is to measure the clear aperture of the lens and draw a circle TWICE this diameter on a piece of card. Then, when the lens is held up to the Sun (the Sun is so far away that the light we receive from it can be considered parallel) and the card is moved back and forth until the bright circle formed by the lens just fills the drawn circle, the distance between the lens and the card is the focal length of the lens. (This procedure is necessary as the Barlow lens is a diverging lens and will not form an image as a convex lens would.) As a rule of thumb, Barlow lenses are generally 75 to 100 mm (negative) focal length.
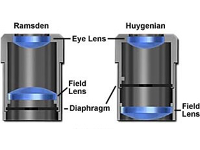
The diagram below shows that there is no fixed relationship between the focal plane of an eyepiece (where the "field stop" or diaphragm is) and the shoulder on the outside of the tube that limits how far into the focuser the eyepiece fits. In the Ramsden eyepiece (left) the focal plane (at the diaphragm) is outside the field lens, but in the Huygenian (right) it is between the two lenses. Thus, when an eyepiece is coupled to a Barlow lens, it is not possible to guarantee where the focal plane of the former will lie in relation to the latter and, because of this, the amplification factor must be considered an approximation.
Variation in position of the focal plane of an eyepiece relative to the external shoulder.
Further, if we alter the distance between the Barlow lens and the eyepiece we change the amplification factor. Increasing the distance increases the amplification factor and this can be done by inserting an extension tube (or star diagonal) between the Barlow lens and eyepiece. For example a 2x Barlow can be changed into a 2.5x or 3x model by this method. Experimentation and measurement will be necessary to determine the new factor. As a guide, a star diagonal can be expected to add a little more than the size of its fitting to this distance, thus a two inch diagonal will add around 60 mm and an inch-and-a-quarter around 35 mm. (This is because there is always a small distance between the two tubes attached to the body of the diagonal and its vertex as well as the length of the light path through the diagonal.) Similarly, decreasing the distance between the Barlow lens and the eyepiece will decrease the amplification factor. This can sometimes be achieved by unscrewing the Barlow lens from its holder and screwing it directly into the end of the eyepiece barrel. Alternatively a different extension tube can be used.
The following formula expresses the Barlow amplification factor, M, in terms of the position of the lens relative to the original focal plane of the objective:
M = f / (f - d) = 1 / (1 – d/f),
where M is the Barlow amplification factor, f is the focal length of the Barlow lens, and d is the distance of the Barlow lens inside the original focal plane of the objective.
The following graph depicts M as a function of the ratio d/f. The amplification is unity when the Barlow is placed in the original focal plane, negative when placed outside it and positive when placed inside it (as would normally be the case). As the Barlow is placed inside the focal plane by a distance equal to its focal length, the amplification becomes infinite and it is no longer possible to focus the image. This provides a limit on where the Barlow lens can be placed.
Barlow amplification as a function of position of lens.
So, does the Barlow lens have any disadvantages? Well, yes, there are at least two. Firstly, placing additional pieces of glass between the objective and eyepiece will cause a little loss of light (typically around 3%). Secondly, in practical terms, a Barlow designed to work at 2x may not work well, or at all, at 5x, for example.
A Barlow lens is typically mounted in a tubular holder that defines the spacing between optical elements as follows:
The Barlow lens increases the effective focal length of a telescope, and the new focal plane of the eyepiece is thus further from the objective than the original. There is a case where this can be advantageous.
One problem with the Tomline Refractor is that the focal plane of the objective is close to the rear end of the optical tube. This means that it is not possible to use a star diagonal as the focussing tube cannot be wound far enough inwards to accommodate the additional light path required. Maybe a Barlow lens would help to overcome this?
To try to answer the question, I decided to experiment. To minimise the "unwanted" amplification provided by the Barlow lens I unscrewed the lens from its tubular holder and attached it to the nose of the diagonal. The light path through the diagonal was slightly longer than the length of the Barlow lens tube: the increase was from around 110 mm (the (negative) focal length of the Barlow) to approximately 130 mm. This increased the power of the Barlow from 2.0x to around 2.2x. I also used the longest focal length eyepiece available, namely 40 mm.
Now, without a Barlow lens, the focal length of the objective (3895 mm) divided by the focal length of the eyepiece (40 mm) gives the magnification of the system as 97x. I confirmed this figure using the technique of dividing the diameter of the objective (258 mm) by the diameter of the exit pupil (around 2.6 mm) to give a figure of 99x. (A Berthon's Dynamometer could be used to measure the exit pupil). The maximum usable magnification of a telescope is often quoted as double the aperture in millimetres; for the Tomline Refractor the figure is approximately 500x. The equivalent minimal focal length of an eyepiece is just under 8 mm (3895/500). Using a 40 mm eyepiece, this equates to a maximum Barlow amplification factor of approximately five (40/8). The Barlow, of course, raises the minimum focal length of eyepiece that may be used.
The ultimate of the above approach would be to place the Barlow lens at its focal length inside the focal plane of the objective, to produce parallel (collimated) light. A "focal reducer" would be necessary re-converge the light (and recreate the eyepiece focal plane) to produce an image.
Experimentation on the Tomline Refractor, undertaken on the evening of 15 April 2015, was successful, for the first time enabling the use of a 50 mm star diagonal with a 40 mm FL, 50 mm aperture eyepiece (see images below). This configuration makes the telescope considerably easier to use when observing objects near the zenith.
Bill Barton, FRAS